Аеропрофил

Цртеж попречног пресека узгонске

површине је обрис аеропрофила.

Попречним пресеком стварне узгонске
површине (крила), добије се
обрис аеропрофила.

Аеропрофил је облик попречног пресека узгонске површине, у равни непоремећене струје флуида, који га опструјава (пресек крила, крака елисе, лопатице турбине итд). Аеродинамика аеропрофила је иста као и крила бесконачне виткости, без утицаја крајева. Генерисање узгона, на аеропрофилу, последица је несиметричног опструјавања, оствареног са геометријском асиметријом и са поставком истог под нападни угао. Остварује се разлика расподеле брзине на горњој и доњој страни, па и разлика притиска, што резултује са силом узгона. На расподелу локалних брзина утиче геометрија аеропрофила: заобљеност носног дела, релативна дебљина и закривљеност. Раније су се аеропрофили дефинисали са процесом физичког обликовања и аеротунелског истраживања, проверавања, доказивања и стандардизовања. На такав класичан начин, развијене су велике серије аеропрофила NACA, ЦАГИ итд. Сада се аеропрофили рачунарски, софтверски моделирају, према унапред задатим аеродинамичким карактеристикама, а у аеротунелима се потврђују и доказују.

Основа

Узгонске површине имају широку техничку примену, као што су крила, ротори и репне површине летелица, елисе, хидрокрила на пловилима, крила за узгон на доле на аутомобилима, лопатице турбина итд. Заједничка им је карактеристика да су им попречни пресеци, дуж размаха, аеропрофили одређеног облика.

Илустрација опструјавања око
ламинарног аеропрофила.

 

Илустрација турбулентног

опструјавања око аеропрофила.

Свако тело са асиметричним опструјавањем ваздуха, или неког другог флуида, генерише силу узгона. Несиметрично опструјавање може бити последица асиметрије облика тела, долазак струјнице под неким углом, у односу на тело, или комбинација. Са асиметријом тела и са нападним углом, подешава се ефективно генерисање силе узгона.

Аеропрофили имају дугачку историју употребе. Још је Лилијентал, у периоду првих експеримената лета са машинама, приметио да закривљена плоча ствара већи узгон од равне. Све до 1915. године, аеропрофили су се пројектовали искуствено и од ока, према интуицији. Средином Првог светског рата, у Немачкој у Гетингену почело је прво систематизовано испитивање аеропрофила. То су били аеропрофили које је Жуковски развио са конфорним пресликавањем. Према институту у Гетингену ти аеропрофили су носили ознаке G, као на пример G.387 и G.398. У САД, Макс Мунк (ен. Max Munk) је, 1926. године, развио серију од 27 аеропрофила, који су детаљно испитани. Касније је НАСА систематизовано приступила развоју аеропрофила.

У првој половини двадесетог века још увек није била расположива теорија за озбиљније рачунско моделирање аеропрофила, а нису ни постојали рачунари за такав задатак. Тада се сводило пројектовање аеропрофила на поступак дуготрајних експерименталних истраживања у аеротунелима. Са развојем теоријских метода моделирања и рачунарске технологије, дошло се до рачунарских поступака са којима се добија геометрија аеропрофила, за претходно задате аеродинамичке услове, на било коме пресеку крила авиона. При пројектовању авиона, изаберу се битнији пресеци крила, на којима се одреди геометрија аеропрофила, па се између два суседна изврши графичка или рачунарска интерполација свих осталих.

На слици десно, приказана је функција коефицијента узгона од нападног угла, за један типичан аеропрофил, који је стандардизован према расположивим алатима у датом времену. Мерење коефицијента узгона је вршено у аеротунелу, у функцији промене нападног угла. Пад узгона, после горње крање превојне тачке, објашњава се са одвајањем ваздушне струје, од горњаке аеропрофила, после критичног нападног угла.

Пројекат аеропрофила, основни је проблем аеродинамике авиона. Избор аеропреофила је везан за оптимизацију режима лета дотичне летелице.

Илустрована зависност коефицијената

узгона и отпора аеропрофила,

у функцији измене нападног угла.

Са асиметричним аеропрофилом, може се генерисати узгон и са нападним углом од нула степени, док са симетричним се исто лети на леђима (у акробацијама), као у нормалном положају.

Симетрични аеропрофил може се користити у већем дијапазону нападних углова, без појаве одвајања ваздушне струје. Трисонични аеропрофили имају заобљену нападну ивицу, која треба бити мање осетљива на промену нападног угла. За средње вредност Рејнолдсових бројева, још пре појаве максималне дебљине граничног слоја, долази до одвајања струје. Суперсонични аеропрофил има оштру предњу ивицу, праве изводнице и има многоугаони облик и веома је осетљив на повећање нападног угла.

Савремени авиони имају променљиве аеропрофиле, дуж размаха, тако да сваки оптимално одговара потребама дела крила на коме се налази.

Аеропрофили за ламинарно струјање имају максималну кривину на 50% тетиве. Међутим, ламинарна функција струјања је угрожена са сваком нечистоћом на додирној површини, као што је киша, инсекти итд.

Геометријски параметри

Основне геометријске и аеродинамичке карактеристике аеропрофила, приказане су на наредним цртежима и у набројању, испод.

Основне геометријске и аеродинамичке карактеристике аеропрофила су:

Класификација

По облику

Визуелна разлика, у општем изгледу, аеропрофила се односи на величину, облик закривљеност и симетричност. Према тим оклностима, деле се на:

• Конкавно-конвексни, после предњег заобљеног дела, горња контура је конвексна (испупчена према напољу) а доња је конкавна (удубљена према унутрашњем делу). Овакав облик је коришћен на старим авионима, а задржала му се употреба на ултралаким авионима.
• Модерни конкавно-конвексни, побољшан је и има одличне перформансе на малим брзинама. То је обично ламинарни профил и доста се користи за узгонске површине једрилица.
• „Клавир“ конвексни, горња контура је испупчена напоље, а доња је равна. Компромисно је решење, због јефтиније производње. Задржао се код авиона са ниском ценом.
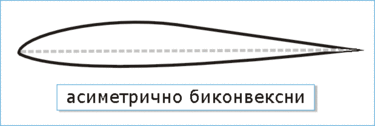
• Асиметрично биконвексни, обе контуре су испупчене, с тим што је горња израженије. Овај облик се користи на већини садашњих авиона.
• Симетрично биконвексни, обе стране су индентичне, а асиметрично опструјавање се постиже само са поставком под нападни угао. Користи се искључиво на високо акробатским авионима, пошто обезбеђује једнаке карактеристике авиона у два супротна положаја (нормалан и леђни).
• Ламинарни, су аепрофили, који, без обзира на своју дебљину не могу да одржавају турбулентно струјање преко одређеног дела своје дужине. Ова функција се остварује са померањем максималне дебљине аепрофила ближе излазној ивици. У поређењу са класичним аепрофилом, омогућава ламинарни гранични слој на већој дужини. Ламининарни аеропрофили генеришу мањи отпор, али само у ограниченом распону нападних углова.

Подкритични

За више информација видети чланак Аеродинамика.

У крозвучној области брзина струјања ваздуха око аеропрофила, на местима повећане кривине контуре нарасте локална брзина до брзине звука. На томе месту се појављује локални ударни талас, а тадашња брзина непоремећене ваздушне струје је еквивалент критичног Маховог броја. Појава локалних ударних таласа изазива пораст отпора и пад градијента узгона. Увек се тежи одложити та појава на веће брзине и сузити распон брзина тога процеса, до потпуног преласка у надзвучно струјање.

У циљу реализације овог циља пројектују се подкритични аеропрофили, којима је критични Махов број висок, што је могуће ближи јединици. У општем случају те аеропрофиле карактеришу:

• Оштрија нападна ивица, са мањим радијусом преласка, да би се смањило убрзање ваздушне струје;
• Место максималне дебљине се помера уназад (око половине тетиве), кривина горњаке се смањује и ублажује се локално убрзање струјања ваздуха.

Ове специфичности, у односу на класични аеропрофил, нису баш много уочљиве, на први поглед (слика доле десно).

Надкритични

За више информација видети чланак Аеродинамика.

Надкритични аеропрофили се користе на режимима лета изнад критичног Маховог броја, односно на авионима чији режими лета су на надзвучним брзинама. Надзвучно локално струјање на горњаци аеропрофила се одлаже и ублажује, тако да су мањи губици енергије, односно да је што мањи пораст таласног отпора.

Стандард–норме

Више од 1.800 аеропрофила, стандардизовано је и користи се у серијској производњи авиона, раније свих а сада углавном цивилних. Највећа је породица NACA, са индефикацијом са 4 или 5 бројева.

• Значење 4-бројчаних ознака (нпр. NACA 2415):
  • 1^и број је вредност максималне кривине у процентима дужине тетиве (нпр. 2 → 0,02 l );
  • 2^и број је удаљеност максималне кривине у процентима дужине тетиве (нпр. 4 → 0,4 l );
  • 3^и и 4^и број означава релативну максималну дебљину, у процентима дужине тетиве (нпр. 15 → 0,15 l ).
• Понекад се 4-бројчани аеропрофили и додатно означавају, као нпр. NACA 2415-24. Додатни бројеви значе:
  • 5^и број значи радијус врха у процентима дужине тетиве (нпр., 2 → 0,02 l );
  • 6^и број значи удаљеност максималне дебљине од врха, у процентима дужине тетиве (нпр. 4 → 0,4 l ).
• Значење 5-бројчаних ознака (нпр. NACA 23012):
  • 1^и број помножен са 3 / 20 представља коефицијент узгона за који је аеропрофил пројектован;
  • 2^и и 3^и број дефинишу релативну максималну дебљину, у процентима од дужине тетиве (нпр. 12 → 0.12 l).

Од врха, према доле, легенда:

• ламинарни аеропрофил за летеће моделе;
• ламинарни аеропрофил за спортске
такмичарске авионе;
• ламинарни аеропрофил за кракове
елиса авиона;
• ламинарни аеропрофил за линиске авионе;
• стабилни аеропрофил за летеће крило;
• трансонични, подкритични аеропрофил;
Легенда:
• Црно = ламинарно струјање,
• Црвено = турбулентно струјање,
• Грао = подзвучно струјање,
• Плаво = суперсонично струјно поље

 

Теорија танког аеропрофила

Теорија танког аеропрофила је једноставна, односи се на везу узгона и нападног угла, у нестишљивом струјном пољу. Развио ју је немачки математичар Херман Глаурт. Заснива се на идеализацији дводимензијалног протока око танког аеропрофила. Чак се сматра да је аеропрофил нулте дебљине, на крилу бесконачног размаха. Ова теорија има важност зато што пружа теоретску основу за важне особине дводимензионалног струјања:

• код симетричног аеропрофила, центар потиска ие на једној четвртини од дужине тетиве,
• код закривљеног аеропрофила центар потиска лежи на једној четвртини дужине тетиве и
• градијент узгона у функцији нападног угла је 2π по једном радијану.

Коефицијент узгона за закривљени аеропрофил је :

– коефицијент узгона, при нултом нападном углу

Теорија танких аеропрофила се користи за нападне углове само до десетак степени.

Приказ теорије танког аеропрофила

За више информација видети чланак Узгон.

У овој теорији се аеропрофил сматра да је танак као линија y(x) и да генерише циркулацију. Продукт циркулације је угаона брзинадуж линије тетиве l.

Пошто не постоји проток по нормалној закривњеној контури аеропрофила,  је компонента главног тока који је локално нормалан на раван – главни ток се локално повије у раван од угла α − dy / dx.

Па је:

Ова једначина са интегралом се решава по после замене x са као и са развојем у ред Фуријера, добија се са модификацијом по времену добија се

Коефицијенти су:

Према теореми Жуковског узгон је пропорционалан изразу: а момент →

Израчунавање коефицијента узгона зависи само од прва два члана Фуријеовog реда

Коефицијент момента првенствено зависи само од А0, А1 и А2

За тачку на 1 / 4 тетиве биће:

Из овога следи да је центар потиска је у тачки 0,25 l ("четврт-тетиве"):

Произилази да је то и аеродинамички центар, а то је тачка на четврт-тетиве. То је место где момент не зависе од нападног угла, односно од узгона:

Види још

Извори